Introduction
Given {1, 2, 3, , , n}, they are all arranged in n!, which is the most basic combination of high school mathematics. Let us take n=4 as an example, all of which are arranged as shown below (in the form of a lexicographic tree):
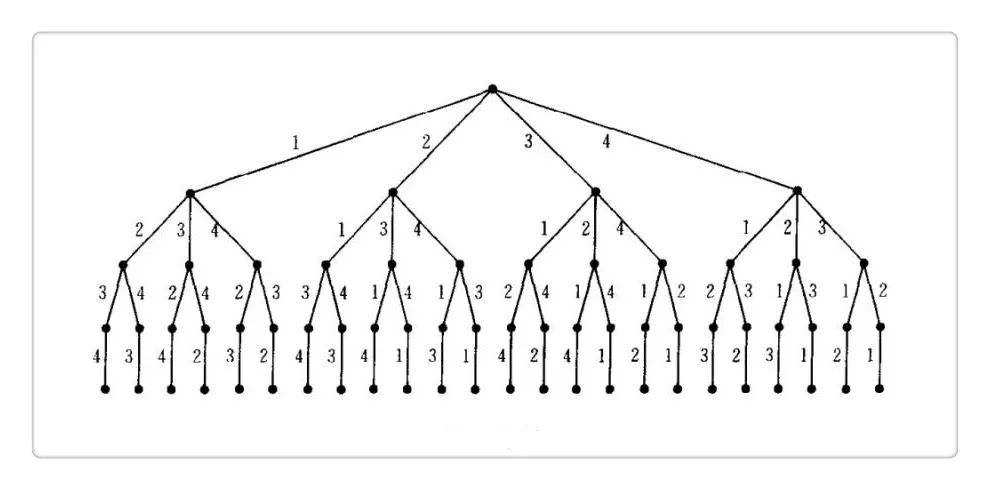
It's easy to think of recursiveness to find all its permutations.
Look closely at the picture above,
Start with 1 followed by the full arrangement of {2, 3, 4};
Start with 2, followed by a full array of {1, 3, 4};
Start with 3 followed by a full array of {1, 2, 4};
Start with 4 followed by the full arrangement of {1, 2, 3}.
code show as below:
/**
*
* author : Liu Yi (Limer)
* date : 2017-05-31
* mode : C++
*/
#include
#include
Using namespacestd;
voidFullPermutation(intarray[], intleft, intright)
{
If(left == right)
{
For(inti = 0;i < 4;i++)
Cout << array[i] << " ";
Cout << endl;
}
Else
{
For(inti = left;i <= right;i++)
{
Swap(array[i],array[left]);
FullPermutation(array,left + 1,right);
Swap(array[i],array[left]);
}
}
}
Intmain()
{
Intarray[4] = {1,2,3,4};
FullPermutation(array,0,3);
Return0;
}
Run as follows:

å’¦~ The recursively written full arrangement is a bit imperfect, it does not strictly follow the lexicographical order. But friends who are familiar with C++ definitely know another simpler, more perfect way to arrange.
Defined in the file
1, next_permutation, for the current permutation, if there is still the next permutation in the lexicographical order, return true, and adjust the current permutation to the next permutation; if not, adjust the current permutation to the first in the lexicographical order Arrange (ie, incrementally) and return false.
2, prev_permutation, for the current permutation, if there is still a previous permutation in the lexicographical order, return true, and adjust the current permutation to the previous permutation; if not, adjust the current permutation to the last permutation in the lexicographical order (ie decrementing), returning false.
/**
*
* author : Liu Yi (Limer)
* date : 2017-05-31
* mode : C++
*/
#include
#include
Using namespacestd;
voidFullPermutation(intarray[])
{
Do
{
For(inti = 0;i < 4;i++)
Cout << array[i] << " ";
Cout << endl;
}while(next_permutation(array,array + 4));
}
Intmain()
{
Intarray[4] = {1,2,3,4};
FullPermutation(array);
Return0;
}
Run the screenshot omitted. The output is exactly in lexicographical order.
How did this "wheel" do it? (Excerpt from Hou Jie's "STL Source Analysis")
1, next_permutation, first, look for two adjacent elements from the very end, so that the first element is *i, the second element is *ii, and *i < *ii is satisfied, find such a group of adjacent elements Then, start from the end to test, find the first element larger than *i, make *j, reverse the i, j elements, and then reverse all the elements after ii, which is what you want "Next" arranges the combination.
2, prev_permutation, first, look for two adjacent elements from the very end, so that the first element is *i, the second element is *ii, and *i > *ii is satisfied, find such a group of adjacent elements Then, start from the end to test, find the first element smaller than *i, make *j, reverse the i, j elements, and then reverse all the elements after ii, which is what you want "Previous" arranges the combination.
code show as below:
Boolnext_permutation(int * first, int * last)
{
If(first == last)returnfalse; // empty interval
Int * i = first;
++i;
If(i == last)returnfalse; // only one element
i = last;
--i;
For(;;)
{
Int * ii = i;
--i;
If(*i < *ii)
{
Int * j = last;
While(!(*i < *--j)) // Look forward from the end until you encounter an element larger than *i
;
Swap(*i, *j);
Reverse(ii,last);
Returntrue;
}
}
If(i == first) // The current arrangement is the last permutation of the lexicographic order
{
Reverse(first,last); // all reverse alignment, which is ascending
Returnfalse;
}
}
Boolprev_premutation(int * first, int * last)
{
If(first == last)returnfalse; // empty interval
Int * i = first;
++i;
If(i == last)returnfalse; // only one element
i = last;
--i;
For(;;)
{
Int * ii = i;
--i;
If(*i > *ii)
{
Int * j = last;
While(!(*i > *--j)) // Look forward from the end until you encounter an element larger than *i
;
Swap(*i, *j);
Reverse(ii,last);
Returntrue;
}
}
If(i == first) // The current arrangement is the first permutation of the lexicographic order
{
Reverse(first,last); // all reverse alignment, ie descending
Returnfalse;
}
}
Post-word
This article focuses on two methods for solving the problem of permutation of non-repetitive sequences: recursion and lexicographical methods.

About this project
ADVANCED SAFE CHARGING: The USB-C MacBook Pro Charger Power Adapter combines advanced safety features and premium fire-resistant materials with built-in protection against overheating, overcharging, overcurrent, and overvoltage.Fast Charge with PD 3.0: The USB C charger features a Thunderbolt 3 USB C port for full-speed charging, charging a 16-inch MacBook Pro in just 1 hour and 30 minutes. (Note input: AC 100-240V-1.5A(1.5A), 50-60Hz, output: 20.5V=4.7A, 15V=3A, 9V=3A or 5.2V=2.4A.
Wide Compatibility: Macbook Charger is compatible with Mac Pro 16 15 14 13", Mac Air 13", i-Pad Pro 11"/12.9", and also compatible with other USB-C enabled devices. Such as laptops, cameras, smart watches, mobile phones, tablets, game consoles, headphones, Nintendo Switch, etc.
GREAT ALTERNATIVE USB-C CHARGER: This compact USB C laptop charger is designed with a foldable plug for easy portability and convenient home/office and outdoor charging.
What you get: USB C Charger Add a free 6.6" USB-C to USB-C charging cable, compatible with Macbook Pro, Mac book Air, iPad Pro, it's more sturdy, super durable, tangle-free, with a lifespan of over 10000 Second-rate.
usb c charger for macbook,macbook usb c charger,usb c macbook adapter,usb c macbook power adapter
Shenzhen Waweis Technology Co., Ltd. , https://www.waweisasdapter.com